Building a secondary index of 1.5 million words for search and auto-complete using Redis cache
Recently I was playing around with building a secondary index for some documents to make them easily searchable using a search interface with auto-complete suggestions. I was interested to explore Redis for this task because it stores data completely in-memory. Though it is a simple Key-Value store with O(1) GET and SET operations, it provides many additional data-structures like Sorted Set, Hash Set, FIFO Queue etc. Moreover, it provides a simple protocol for communication over raw TCP (and UNIX) sockets - all these factors makes Redis a suitable candidate for building secondary indexes that reside completely in memory and can be used for retrieving results really quickly (with microsecond latencies). In this post, I will explain how we can exploit Redis to store large indexes for search and auto-complete and how we can further optimize it to scale the solution.
The problem of prefix-search
The problem here is simple, given a list of N words, how will you search for a given word in that list quickly? Extending this problem further, how will you get a list of M words that start with the given prefix? (example: If I have words - [banana, bayer, bay] then the prefix bay should return [bay, bayer], similarly the prefix ba should return [banana, bayer, bay]) - In Computer Science, this is called “Prefix Search”, because in a large search space of N strings, you are finding a set of M strings that start with the given prefix (M <= N), the naive way to solve this problem is to iterate over all the strings one at a time and checking if it has the given substring as it’s prefix, for that we can use strcmp() or memcmp() - this solution is trivial, it works the best if we have a smaller search space, but this solution doesn’t scale well if we have larger search space (like millions of words) because this is a O(N) solution, as N increases the time taken to search also increases linearly, to scale the solution well, we need a data-structure that takes less than O(N) time. The most efficient way to tell if a string is present in the given set is to use hash-table, we hash the string, if that hash is present in the table, then it exists - this is an ideal way of search where the time-complexity is almost O(1) in most of the cases, this solution scales well, but it fails to solve our problem, our problem here is to obtain a subset of strings that start with the same prefix in a given large set of strings.
Trie - a naive prefix search tree:
In the previous section we looked at O(n) solution which actually solved the problem, but not scalable, we also saw O(1) solution that is scalable but didn’t actually solve the problem. One of the possible solutions that is slower than hash-table and faster than linear search is to use a trie. Trie data-structure is also known as prefix-tree. In simple words, every parent in the prefix tree is a prefix of the child. (i.e if we have two words ban and bay then the tree has a structure b->a->(n, y), b is the prefix of a and ba is the prefix of n and y, so all the parents in that path is a prefix of the upcoming children in the same path). Here is a representation of prefix tree:
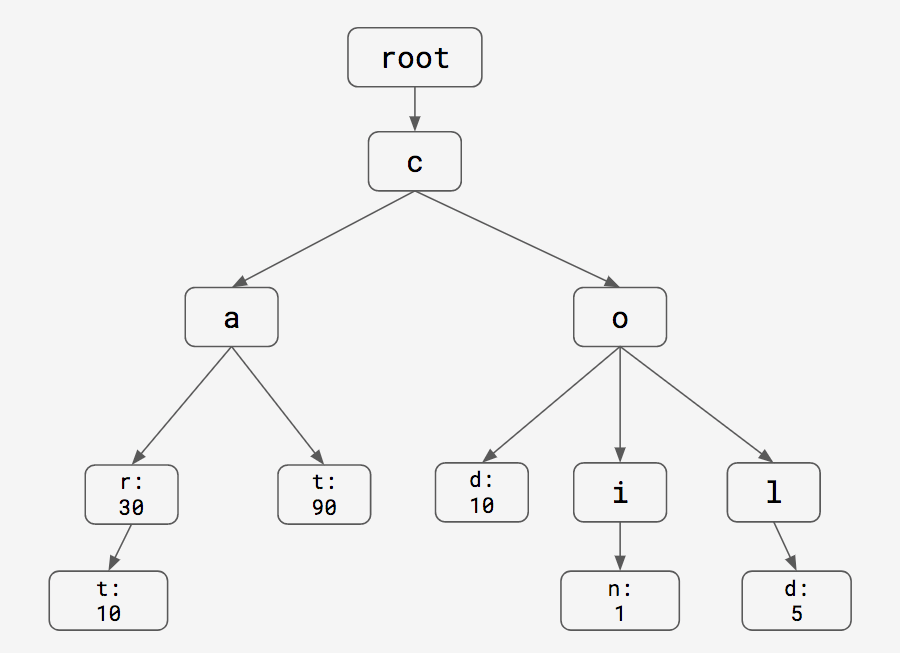
The above trie can be used for efficient prefix search on words [cart, car, cat, cod, coin, cold]. Once we have a prefix, we can traverse one node at a time based on each character in the prefix (if it exists in the trie), once our prefix ends we can do depth-first-search (or DFS) traversal over all the children starting from the node where our prefix ended to obtain all the possible strings that has the given prefix. This solution has time-complexity O(M) + O(P + E), where M is the length of the prefix, P is the number of nodes that are in the sub-tree starting from the last prefix node and E is the number of edges involved in the sub-tree on which DFS is applied. (Note: Here the time-complexity of DFS is O(P + E) which has been added to O(M), if we ignore the edges, then the time complexity is O(M) + O(P)), if you consider the time-complexity only to search the prefix then it is O(M). This looks fine the time-complexity is far better than O(N), but this is not always better, because most of the prefix search problems have smaller M value (i.e smaller prefix length), for example if I have 10000 strings in a set all starting with prefix b->a, then using ba as the prefix will lead to negligible O(M) and higher O(P + E), but this is far better solution than linear search. This problem can be avoided by using an additional hash-table that stores list of all prefixes as keys and each key has a list of strings that starts with the given prefix as value, by this way we can avoid O(P + E) component in our prefix search, a similar approach has been suggested here, this data-structure is called Prefix-Hash tree. The diagram below shows how a prefix-hash tree looks like for the set of six words - [cart, car, cat, cod, coin, cold]
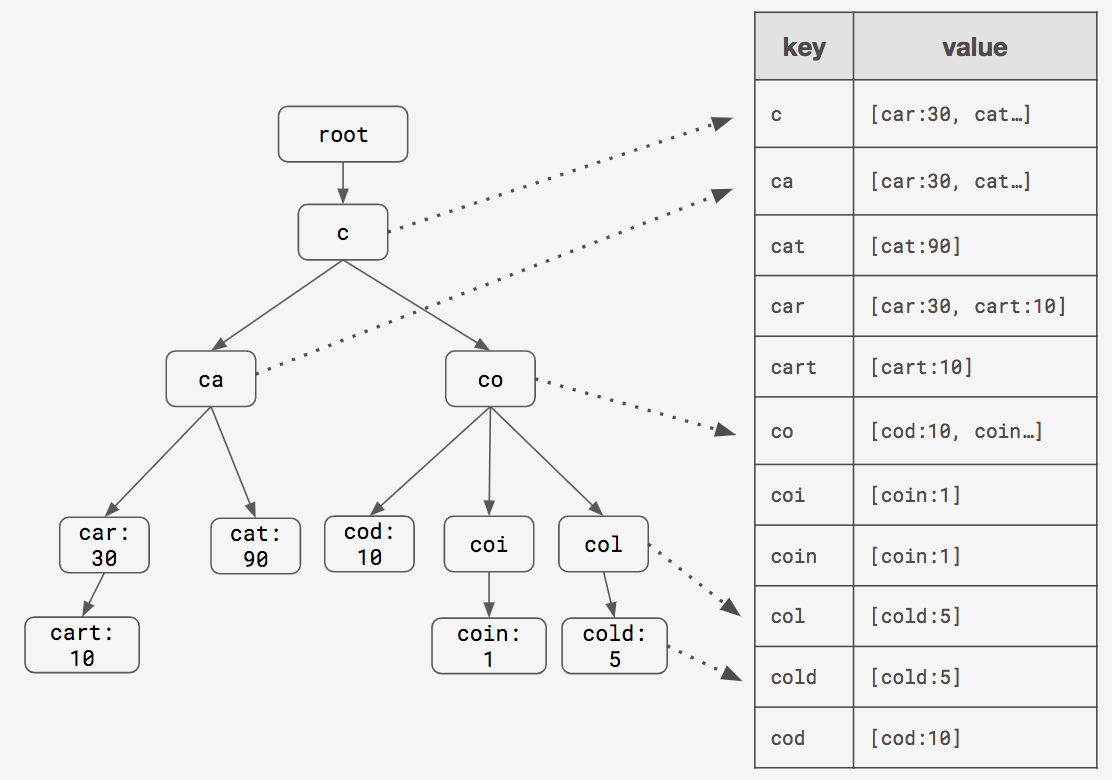
While this data-structure is highly efficient than a naive trie (time-complexity: O(M) + O(1)), it consumes lot of memory - it can be noted from the above diagram, we are duplicating the strings across multiple locations in the hash-table. (Imagine the size of this table for 10000 words). In the coming sections, we will see how Redis Sorted sets can be used for solving this problem with some compromise on the time complexity.
Redis sorted sets
We looked at various approaches for prefix-search in previous sections, now let us implement one using Redis. As mentioned earlier, Redis is a in-memory key-value store. It provides many data-structures like Sorted set, FIFO Queue, Hash set etc. A simple solution is to insert each string as a key with some dummy value (for example banana:1, apple:1, applied:1) into the key-value store (we can use SET command), this solution has O(1) time complexity for checking whether the given string exists or not, this is done by hashing the string and checking it against the key-value store, which is implemented using a hash-table (using GET command), but this method cannot be used for prefix search, for this we need to scan the entire key-value store using <prefix>* regular-expression, this can be done using SCAN command, the time complexity is O(N) because this approach is nothing but a linear search performed on all the keys in the hash-table. What we actually need is a data-structure that provides time-complexity lesser than O(N), fortunately Redis provides Sorted Set, which provides O(logN) time-complexity insertion, deletion and retrieval. Sorted sets also called as zsets are built using combination of two vanilla data structures - Hash Tables and Skip-Lists. Skip-Lists improve the efficiency of linear linked list traversal by allowing us to skip unnecessary nodes in between and start from a point where the element we are looking for is more likely to be present, this is made possible by having another metadata linked list that contains nodes storing pointers to convenient nodes in the main linked list from where we can start traversal to find a given element, by this way it reduces the search space by avoiding a linear search over all the nodes. Here is an example:
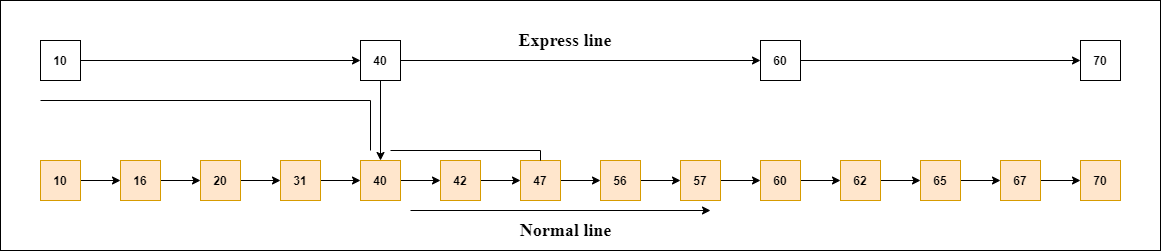
In order to search 56 in the given linked list, we can traverse the Express Line first , the Express line also called as Metadata List contains pointers intermediate locations on the main list. Since nodes are sorted in increasing order on the main list, we can be sure that node 40 is the probable starting point because 40 < 56 < 60 so we skip to node 40 directly on the main list instead of starting from 10, by this way we can avoid unnecessary traversal from 10 to 40 on the main list. The efficiency of skip-list varies based on the number of nodes we have in express line, if there are no nodes in express line, then the time complexity is O(N) as more and more nodes are added to the express line, the efficiency improves, we can also have multiple levels express lines with pointers tp multiple locations to improve the speed (read this paper to understand the concept behind skip-lists completely). Skip-list can be approximated to a completely balanced binary search tree (BST) in it’s best case. In general it is a balanced tree with O(logN) as the time-complexity for search (traversal).
Redis sorted set is implemented on top of skip-list, so it provides O(logN) insertion and search capabilities. To understand how Sorted Sets are implemented, check out the source code - t_zset.c.
Note: I will be using redis-cli for all the commands executed below.
Scores and Lexicographic ordering in Sorted Sets:
Sorted sets in Redis are sorted based on a number called Score (also called as Rank), for example if I insert three strings [banana, bay, bayer] with ranks [2, 0, 1], then they are automatically sorted as [bay:0, bayer:1, banana:2]. Let’s check this out by creating a sorted set by name test (we can insert elements into sorted set using ZADD command and use ZRANGEBYSCORE command to query the sorted set by scores between 0 and 2).
127.0.0.1:6379> ZADD "test" 2 "banana"
(integer) 1
127.0.0.1:6379> ZADD "test" 0 "bay"
(integer) 1
127.0.0.1:6379> ZADD "test" 1 "bayer"
(integer) 1
127.0.0.1:6379> ZRANGEBYSCORE test 0 2
1) "bay"
2) "bayer"
3) "banana"
But can we have multiple entries with same score? Yes, Redis allows this as well, when we insert multiple entries to the sorted set with the same score, they are sorted lexicographically. This ordering is performed at bytes-level so any data type can be sorted lexicographically by comparing their raw bytes representation (using memcmp()). For example, let us try inserting [pickle, pineapple, poet, pi, pin, pot, pen] to a sorted set called “test2” with same score 0.
127.0.0.1:6379> ZADD "test2" 0 "pickle"
(integer) 1
127.0.0.1:6379> ZADD "test2" 0 "pineapple"
(integer) 1
127.0.0.1:6379> ZADD "test2" 0 "poet"
(integer) 1
127.0.0.1:6379> ZADD "test2" 0 "pi"
(integer) 1
127.0.0.1:6379> ZADD "test2" 0 "pin"
(integer) 1
127.0.0.1:6379> ZADD "test2" 0 "pot"
(integer) 1
127.0.0.1:6379> ZADD "test2" 0 "pen"
(integer) 1
127.0.0.1:6379> ZRANGEBYSCORE test2 0 0
1) "pen"
2) "pi"
3) "pickle"
4) "pin"
5) "pineapple"
6) "poet"
7) "pot"
If you see the above example, though elements were inserted in a different order, they appeared in a lexicographically sorted order. We can use the command ZRANGEBYLEX to also perform range queries on this sorted set, lets see few examples of how we can use ZRANGEBYLEX command:
127.0.0.1:6379> ZRANGEBYLEX test2 "[pi" "(pj"
1) "pi"
2) "pickle"
3) "pin"
4) "pineapple"
127.0.0.1:6379> ZRANGEBYLEX test2 "[pin" "(pio"
1) "pin"
2) "pineapple"
Here is what we did, we performed range query on the sorted set (here [ means inclusive and ( means exclusive) to obtain the list of all strings that has the prefix pi (using [pi) in example 1 and pin (using [pin) in example 2, since this is a range query, we use upper limit (pj and (pio respectively. This query simply means, get all the strings until we do not find prefix pi and pio respectively. Let’s dive deep and understand how this actually works, first given a prefix as string, the sorted set is searched for that string, the time complexity of this search is O(longN) because sorted set is built using skip-list data structure. Once we find the prefix in the list, we scan from that position until the next string has a different prefix. Lexicographic sorting has a major role to play here because it makes strings with same prefix appear next to each other forming a cluster. The time-complexity is O(logN) + O(M) where O(longN) is the time-complexity of skip-list prefix search and then O(M) is the time-complexity involved in scanning next M elements having the same prefix. (If there was no lexicographic sorting, then the time-complexity would have been O(M * logN) because we need to perform search on the entire set M number of times). If we want all the strings having the same prefix then the value of M is unknown and we have to take that into account, but if we limit M i.e if we say we only need first M strings having that prefix then M is constant, in that case the time-complexity is O(logN). Sorted sets are efficient than prefix-hash trees we saw in previous sections because sorted set by default doesn’t allow duplicates, each string appears exactly only once in our data-structure, moreover sorted sets are faster as well (though not as fast as Prefix-hash trees) - these characteristics of sorted sets make it scalable (in terms of both time and space).
Let’s experiment!
In this experiment we will create a sorted set comprising of 1516217 words (roughly equal to 1.5M). There is a github repository that hosts around 466K words appearing the english dictionary. We will generate the possible prefixes of all these words and add it to the list as well, so together we get around 1.5M words. We will create a python function called get_word_list that downloads words file from github, generates all prefixes and creates a large index out of it.
def get_all_prefixes(word):
perms = [word[0:i] for i in range(0, len(word) + 1)]
perms[-1] = perms[-1] + "*"
return perms
def get_word_list():
try:
data = requests.get("https://raw.githubusercontent.com/dwyl/english-words/master/words.txt")
all_words = data.text.split("\n")[:-1]
print('got ', len(all_words), 'words')
all_words_records = {}
for word in all_words:
perms = get_all_prefixes(word)
all_words_records.update({ perm: 0 for perm in perms })
return all_words_records
except Exception as e:
print('Error getting word list', e)
os._exit(-1)
To distinguish between complete words and prefixes, we append * at the end of a complete word (for example if we have the word bayer then we create the list [b, ba, bay, baye, bayer*] - here bayer is suffixed with * to tell it is a complete and valid dictionary word while others in the list are not). This approach is suggested here. Let’s create a sorted set out of this large index of words:
def create_redis_words_index(index_data):
try:
socket = redis.Redis(
host=REDIS_HOSTNAME, port=REDIS_PORT, password=REDIS_PASSWORD,
db=REDIS_DB
)
# avoid socket write error by writing 100k elements at a time
idx = 0
temp_dict = {}
for k, v in index_data.items():
idx +=1
temp_dict[k] = v
if idx == 100 * 1000:
print('inserting', idx, 'words')
socket.zadd("word_index", temp_dict)
idx = 0
temp_dict.clear()
else:
print('inserting', idx, 'words')
socket.zadd("word_index", temp_dict)
except Exception as e:
print('Redis index build error: ', e)
os._exit(-1)
# call them together
if __name__ == "__main__":
index = get_word_list()
print('Creating index of', len(index), 'entries')
create_redis_words_index(index)
This function should create a Redis socket and push 100k entries at a time (we are limiting to 100k words at a time to avoid putting overwhelming amount of data on the socket at a time). All of these words have same score of 0. If this script runs properly we should see the sorted set word_index created by Redis. Let’s verify this using Redis CLI:
127.0.0.1:6379> ZCOUNT word_index 0 0
(integer) 1516217
By using ZCOUNT we can verify that there are 1.5M entries in our sorted set. Let’s look at the memory
127.0.0.1:6379> MEMORY USAGE word_index
(integer) 130797574
1.5M words take around 131MB of RAM, which is not a problem and shouldn’t be a concern for today’s tech world. Now let’s run some search queries on this index:
127.0.0.1:6379> ZRANGEBYLEX word_index "[apple-p" "(apple-q"
1) "apple-p"
2) "apple-pi"
3) "apple-pie*"
4) "apple-po"
5) "apple-pol"
6) "apple-poli"
7) "apple-polis"
8) "apple-polish"
9) "apple-polish*"
10) "apple-polishe"
11) "apple-polisher*"
12) "apple-polishi"
13) "apple-polishin"
14) "apple-polishing*"
In the above example we queried for all words starting with prefix apple-p, we got 14 words in our result and there are four complete words ([apple-pie, apple-polish, apple-polisher, appli-polishing]). Now let’s check the latency (make sure you run CONFIG SET slowlog-log-slower-than 0 command to make Redis log all the commands in it’s slow log):
1) 1) (integer) 22
2) (integer) 1648887228
3) (integer) 52
4) 1) "ZRANGEBYLEX"
2) "word_index"
3) "[apple-p"
4) "(apple-q"
It took us around 52 microseconds, which is great. This latency is not constant, it depends on various internal factors and also on the number of results that were returned as the output. For example if we run ZRANGEBYLEX word_index "[ap" "(aq" the result will have around 4.5K words, in such case we get 1.2 milliseconds of latency. This might be a problem because we have variable latencies, but we can fix this by setting ourselves a limit on the number of results to be returned (remember the M in previous section), let’s try the same command with limit=100.
We can do this by setting LIMIT parameter in our query - ZRANGEBYLEX word_index "[ap" "(aq" LIMIT 0 100. Now let’s look at the latency:
1) 1) (integer) 32
2) (integer) 1648887700
3) (integer) 70
4) 1) "ZRANGEBYLEX"
2) "word_index"
3) "[ap"
4) "(aq"
5) "LIMIT"
6) "0"
7) "100"
We got 70 microseconds latency to get first 100 matches. Let’s write a simple python script that makes 1000 requests with different randomly selected queries with limits=(10, 50, 100) to measure the latency:
def exec_cmd_with_time(lim):
queries = [
(b'[fin', b'(fio'), (b'[pa', b'(pc'), (b'[see', b'(sef'),
(b'[appl', b'(appm'), (b'[lo', b'(lp')
]
LIM = lim
try:
socket = redis.Redis(
host=REDIS_HOSTNAME, port=REDIS_PORT, password=REDIS_PASSWORD,
db=REDIS_DB
)
latencies = []
for _ in range (0, 1000):
q = random.choice(queries)
start_q, end_q = q
st = time.time()
socket.zrangebylex("word_index", min=start_q, max=end_q, start = 0, num = LIM)
et = time.time()
latencies.append(et - st)
print('avg latency:', (sum(latencies) / 1000) * 1000, 'ms for LIMIT =', LIM, 'for 1000 runs')
except Exception as e:
print('redis search error ', e)
os._exit(0)
We get the following outputs:
avg latency: 0.15553975105285645 ms for LIMIT = 10 for 1000 runs
avg latency: 0.35407352447509766 ms for LIMIT = 50 for 1000 runs
avg latency: 0.6271829605102539 ms for LIMIT = 100 for 1000 runs
Here we are measuring end-to-end latency, this is roughly the time taken for pre/post processing + pushing data to socket + transmission + execution + sending data back to the same socket + transmission + receiving data all-together. This is practical because we can’t infer anything from just execution time alone for real world applications. (Machine Spec: 4GB RAM, 4 vCPUs, localhost Redis setup, I took a low spec machine purposefully).
Encoding metadata:
Till now we just stored words alone, what happens once we get these words? For that we need some application specific information to be stored along with these words. For example, in documents search use-case we can store the IDs of the documents in which the given word occurs (These IDs will be processed by the application to search object storage or some other database). One simple way is to store them in the string that represents the word itself, for example, the string apple-pie* can have additional information in it’s suffix instead of * like: apple-pie::102 or apple-pie:102:103:110:154, here these numbers separated by :: can be unique IDs of the documents, these encodings will be present only for complete words and not for prefixes. These IDs can be used to query the document DB further when user selects a word from the suggestions (we can hide these IDs from being displayed to the users). If your metadata is more complex, then use HSET to create a hash set and use the complete word as key followed by the metadata as it’s value. In this case we have to make two queries to Redis, one for auto-complete suggestions and another for getting the metadata (list of document IDs) from the hash-set once a word is selected.
Scaling this for millions of words and possible optimizations:
This solution is very naive and there are still many optimizations we can do.
1. Partitioning:
In the case we experimented, all 1.5M words had the same score and were stored in the same sorted set - this results in large N value, so the performance of O(logN) might reduce if we put hundreds of millions of words. One way to avoid this problem is to partition the search space, for this we need to create multiple sorted sets. In our example, we created only one sorted set called word_index, but we can have k sorted sets like [word_index-0, word_index-1, ...., word_index-k], while insertion we can decide to which partition (sorted-set) the word should go to by applying start_letter_of(word) % k, in this case we will have k indexes. We cannot ensure equal distribution across all the k indexes because the words in any language will not be uniform across all the alphabets.
2. Sharding
If our index cannot fit into the memory of a single machine or you want high-availability and good load distribution we can go for sharding (we need multiple machines). We can use the same start_letter_of(word) % k rule to distribute the words across machines. We can keep k as small as possible so the number of machines required will be less (example: k=2 will require two machines and we can have 13-13 split if we have 26 letters, i.e machine-0 - [words starting from a to m], machine-1 - [words starting from n to z]).
3. Most frequently searched index:
We can have few words and their prefixes on a separate sorted set. This set should contain only those words that are most frequently searched (limit the number of unique words that goes into this set), this index can be re-constructed periodically to bring in new words and remove words that are no longer frequently searched (this period can be set to 6 hours, 12 hours or a day based on your requirements). For this we need a analytics DB, this can again be a redis sorted set where the scores are increased every time for that word when it is searched, periodically we obtain words having top M scores and create an index out of those words along with their prefixes so that it can be used as most frequently searched index for prefix-search and auto-complete. This is a probabilistic approach where we first search this index and then the index where we have all the words and their prefixes. This approach can speed up our search most of the time because the most frequently searched word index always contains trending searches for that time period and it has lesser words than the actual large index (this means smaller N value and thus smaller O(logN)).
These are the possible optimization I can think of at the moment.
Conclusion:
In this post, we saw different data-structures that can be used for prefix search and how we can use Redis and it’s data structure Sorted Sets to implement prefix search for our auto-complete search suggestions, we also saw various possible optimizations.